DETECCIÓN DE DAÑOS ESTRUCTURALES UTILIZANDO APRENDIZAJE PROFUNDO Y TÉCNICAS DE ACTUALIZACIÓN DE MODELOS DE ELEMENTOS FINITOS (FE)
Yunwoo Lee, Heesoo Kim, Seongi Min & Hyungchul Yoon
https://doi.org/10.1038/s41598-023-46141-9
Published: 31 October 2023
Traducido por: TheJameZ
La condición estructural puede estimarse mediante varios métodos. La detección de daños, como uno de esos métodos, se ocupa de identificar cambios en características específicas dentro del comportamiento estructural basándose en modelos numéricos. Dado que el método se basa en simulación para diversas condiciones de daño, existen limitaciones en su aplicabilidad debido a discrepancias inevitables entre el modelo analítico y la estructura real. La actualización del modelo de elementos finitos es una técnica para establecer un modelo de elementos finitos que pueda reflejar el estado actual de una estructura objetivo según las respuestas medidas. Se realiza mediante optimización para varios parámetros estructurales, pero el resultado final puede converger de manera diferente según el modelo inicial y las características del algoritmo. Aunque el modelo actualizado puede no replicar fielmente la estructura objetivo tal como es, se puede considerar equivalente en cuanto a la relación entre las propiedades estructurales y las características de comportamiento del objetivo. Esto permite el análisis de cambios en las relaciones mecánicas establecidas para la estructura objetivo. El cambio puede estar relacionado con daños estructurales, y la tecnología de inteligencia artificial puede ofrecer una solución alternativa en problemas complejos donde los enfoques analíticos son desafiantes. Tomando aspectos prácticos de los métodos mencionados, se presenta en este estudio una metodología novedosa de detección de daños estructurales para identificar la ubicación y la magnitud del daño. La actualización del modelo se utiliza para establecer un modelo de referencia que refleje las características estructurales del objetivo. Los datos de entrenamiento para diversas condiciones de daño basadas en el modelo de referencia permiten a las redes de inteligencia artificial identificar el daño en la estructura objetivo.
Existen diversos métodos para evaluar el estado actual de las estructuras. Los métodos más populares que se están utilizando en los sitios son inspecciones manuales en el lugar y monitoreo de la salud estructural basado en vibraciones. Las inspecciones en el lugar involucran la inspección visual y la evaluación manual de los elementos estructurales para detectar daños o anomalías visibles. Aunque proporciona un medio útil para evaluar la condición de la estructura, la precisión y confiabilidad de la evaluación pueden ser subjetivas y propensas a errores humanos. Además, las inspecciones en el lugar generalmente se llevan a cabo en intervalos específicos, lo que significa que la evaluación puede no capturar el comportamiento en tiempo real o la deterioración de la estructura de manera continua.
Por otro lado, los sistemas de monitoreo de salud estructural basados en vibraciones pueden vigilar continuamente el comportamiento y la respuesta de las estructuras mediante sensores y técnicas de adquisición de datos. Estos sistemas de monitoreo de salud estructural analizan los datos recopilados y realizan procesamiento posterior para obtener información útil que pueda hacer referencia a la condición de la estructura. Estos métodos ofrecen una evaluación más completa y objetiva del estado estructural, pueden proporcionar mantenimiento preventivo y respuestas oportunas para mantener la integridad y seguridad estructural.
La respuesta estructural puede analizarse mediante varios métodos para evaluar su condición. Uno de los enfoques más comúnmente empleados es la identificación del sistema estructural basada en vibraciones, que tiene como objetivo extraer parámetros modales y características dinámicas de las estructuras a través del análisis de las vibraciones medidas. Al medir las características dinámicas, se pueden obtener perspicacias valiosas sobre la integridad estructural. Las ventajas de este método incluyen su naturaleza no destructiva, simplicidad de aplicación y la capacidad para capturar respuestas globales.
Existen varios estudios que han intentado estimar el cambio en las condiciones estructurales a través de cambios en las frecuencias naturales utilizando datos de medición a largo plazo. Aunque algunos estudios han demostrado que la frecuencia natural puede proporcionar información valiosa relacionada con la rigidez de las estructuras, no fue suficiente para estimar la condición de las estructuras directamente. En la mayoría de los estudios, la frecuencia natural se utilizó más bien como el parámetro de entrada (característica) de un sistema que se puede emplear para evaluar indirectamente la integridad estructural.
Otro método que se está estudiando ampliamente para el monitoreo de salud estructural basado en vibraciones es la detección de daños. Los métodos de detección de daños no solo encuentran la ubicación de los daños, sino que también estiman la magnitud del daño. La mayoría de los métodos utilizan las diferencias en las respuestas estructurales bajo condiciones dañadas e intactas para detectar el daño. Se pueden utilizar diversas respuestas para identificar las características de comportamiento de la estructura, incluyendo la aceleración, la deformación, el desplazamiento. Una vez que se mide la respuesta de la estructura, se pueden utilizar técnicas avanzadas, incluyendo algoritmos de procesamiento de señales y aprendizaje automático, para detectar el daño. Aunque las características dinámicas como la frecuencia natural y la forma modal generalmente se utilizan como parámetros de entrada para estos procedimientos de postprocesamiento, muchos investigadores han utilizado frecuencias naturales como base para la identificación de la integridad estructural. En los métodos convencionales, se propuso un índice de daño específico para resaltar las características del cambio en la frecuencia natural para la condición dañada. Sin embargo, estos métodos fueron difíciles de derivar un índice que pueda representar suficientemente la magnitud y ubicación del daño a partir de la frecuencia natural mediante un tipo de proceso de cálculo numérico. Además, dado que el método se realiza en base a simulación, existen limitaciones en su aplicación debido a discrepancias en el comportamiento de las estructuras reales.
La actualización del modelo de elementos finitos (FE) es otra forma adicional de evaluar el estado actual de las estructuras. Este método utiliza modelos de elementos finitos para refinar y actualizar el modelo numérico, con el objetivo de lograr una representación más precisa del comportamiento sistemático de la estructura objetivo. Los parámetros del modelo pueden incluir propiedades del material, condiciones de contorno o características geométricas. Este proceso generalmente emplea un algoritmo de optimización que minimiza la discrepancia entre las respuestas simuladas del modelo y las respuestas medidas de sensores o pruebas experimentales. Ajustando iterativamente el modelo, se logra una alineación más cercana con el comportamiento de la estructura objetivo. La frecuencia natural de la estructura sirve como una característica de entrada destacada en este método. Dado que la frecuencia natural es uno de los factores más efectivos que puede representar la relación entre la rigidez y la masa de una estructura, permite que el modelo de elementos finitos converja hacia las características mecánicas de la estructura objetivo. Sin embargo, el modelo actualizado finalmente convergido depende del modelo inicial y las características del algoritmo de optimización, así como de las suposiciones dentro del proceso de actualización. Además, existe una limitación para construir un modelo que pueda replicar todas las características de comportamiento de la estructura, incluido el comportamiento estático, basándose únicamente en características dinámicas. No obstante, aún puede presentar la posibilidad de ser utilizado para identificar cambios en estas relaciones establecidas al optimizar la relación entre las propiedades estructurales consideradas y las características de comportamiento.
En un esfuerzo por abordar los desafíos en un método convencional de detección de daños estructurales, los investigadores han explorado la aplicación de la tecnología de inteligencia artificial (IA). La tecnología de IA puede ofrecer soluciones alternativas basadas en datos para problemas que involucran patrones difíciles de detectar o que no pueden definirse de manera determinista. La eficiencia de las soluciones depende estrechamente de la calidad de los datos de entrenamiento. A medida que se ha desarrollado la tecnología para generar y procesar grandes cantidades de datos, su utilidad se ha mejorado significativamente y se está aplicando en diversos campos. En cuanto al aspecto arquitectónico de la red, se ha utilizado en diversas formas para la detección de daños estructurales. La red neuronal profunda (DNN), como la forma fundamental de una red neuronal, explora la relación entre la entrada y la salida a través de un proceso de avance. Es útil cuando la entrada y la salida pueden definirse de manera relativamente simple. La red neuronal recurrente (RNN), con su estructura recurrente capaz de incorporar información pasada al estado actual, es adecuada para procesar datos secuenciales como datos de series temporales. Datos como la respuesta dinámica de las estructuras pueden utilizarse como entrada para RNN. La red neuronal convolucional (CNN) está especializada principalmente en procesar datos espaciales como imágenes. Se utiliza para extraer características espaciales de los datos y no solo es útil para el análisis de imágenes, sino que también facilita la extensión de características de datos para el análisis. En cuanto a la metodología de entrenamiento, existen métodos supervisados donde las salidas están etiquetadas para las entradas correspondientes con el fin de extraer características para la relación, y métodos no supervisados que descubren patrones a partir de datos sin etiquetas y entrenan automáticamente redes. Los métodos supervisados, al basarse en etiquetas claras, pueden proporcionar un rendimiento excelente para predicciones precisas. Sin embargo, en casos donde es desafiante especificar etiquetas claras, como en las condiciones de estructuras reales, o cuando el objetivo es descubrir nuevas características, los métodos no supervisados pueden ser más apropiados.
Este estudio adopta los aspectos prácticos de las técnicas previamente descritas para su aplicación eficiente en la detección de daños en estructuras reales. Se aplicó una técnica de actualización de modelos de elementos finitos (FE) para construir un modelo de FE capaz de representar adecuadamente las características dinámicas de la estructura objetivo. Posteriormente, se llevaron a cabo simulaciones de análisis estructural para varios casos arbitrarios de daño basados en el modelo de FE actualizado. La tecnología de inteligencia artificial puede ser entrenada con diversas condiciones de daño que pueden ocurrir en la estructura objetivo a través de datos simulados. Dado que el modelo de FE de referencia fue diseñado para reflejar fielmente la estructura objetivo, la red entrenada puede identificar de manera efectiva la ubicación y el grado de daño en la estructura objetivo cuando este ocurre.
El siguiente capítulo ofrece una descripción detallada de la metodología propuesta. La viabilidad de este enfoque se ha confirmado a través de pruebas experimentales, y la discusión integral correspondiente se presenta en la sección "Prueba de validación", que abarca tanto las simulaciones de análisis estructural como el entrenamiento de la red de inteligencia artificial. La sección "Conclusión" incluye un resumen breve y detalla las direcciones futuras de trabajo para el estudio.
METODOLOGIA
Se muestra una descripción esquemática del método propuesto en este estudio en la Figura 1. El método propuesto se puede dividir en tres pasos. El primer paso consiste en construir un modelo de elementos finitos (FE) de referencia que pueda representar adecuadamente el estado actual de la estructura objetivo. Esto se puede lograr mediante la actualización del modelo de FE utilizando propiedades dinámicas obtenidas de la identificación del sistema para la estructura objetivo. En el segundo paso, se generan numerosos modelos de FE dañados de manera arbitraria basados en el modelo de FE de referencia derivado en el paso anterior. Estos modelos se utilizan para entrenar la red de detección de daños para diversas condiciones de daño. La identificación del sistema en la etapa final, cuando ocurren defectos en la estructura, captura las características dinámicas de la estructura dañada. Posteriormente, esta información se aplica a la red de detección de daños para evaluar el estado actual de la estructura. Se describen detalles adicionales de la metodología en las secciones siguientes.
IDENTIFICACION DEL SISTEMA
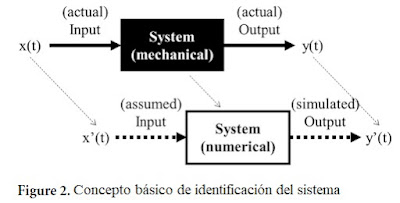
La identificación del sistema se refiere al proceso de determinar un modelo matemático o características de un sistema basado en datos de entrada y salida observados, como se muestra en la Figura 2. Un sistema establece la relación entre la entrada y la salida. Cuando es difícil conocer el sistema mediante enfoques analíticos, las relaciones entre los datos de entrada y salida se pueden utilizar para identificar las características del sistema y establecer un modelo matemático correspondiente al sistema. Sin embargo, en casos en los que la entrada al sistema no es clara, como en estructuras típicas con cargas que actúan de manera compleja, la identificación del sistema solo con salida se puede llevar a cabo asumiendo la entrada como ruido blanco y utilizando solo la respuesta de la estructura.
La identificación del sistema se puede realizar de varias maneras. En ingeniería estructural, generalmente se lleva a cabo mediante el análisis en el dominio de frecuencia de la respuesta de vibración ambiental de la estructura. Los datos de respuesta dinámica de la estructura se transforman utilizando técnicas como la transformada de Fourier para obtener componentes de frecuencia y, luego, aplicando el método de selección de picos, se pueden identificar picos dominantes o frecuencias resonantes. Para el procesamiento de señales digitales típicas, se aplica la transformada discreta de Fourier, como se expresa en la ecuación (1), permitiendo la extracción de componentes de frecuencia de los datos de respuesta dinámica de las estructuras.
Aquí, x es la entrada de datos que se transformará al dominio de frecuencia, N es el número de muestras de la entrada y k denota el índice de frecuencia y tiene valores de 0 a N - 1.
La Función de Respuesta en Frecuencia (FRF, por sus siglas en inglés) es uno de los conceptos fundamentales en el campo de la dinámica estructural, que representa la relación entre la excitación de entrada y la respuesta de salida correspondiente en el dominio de frecuencia. Proporciona información significativa sobre el comportamiento dinámico de un sistema y se utiliza ampliamente en diversas aplicaciones de ingeniería. Definiendo X(ω) e Y(ω) como las transformadas de Fourier de las señales de entrada y salida, respectivamente, la FRF del sistema se puede expresar mediante la ecuación (2).
La FRF sirve como una herramienta valiosa para la identificación del sistema, permitiendo discernir las frecuencias resonantes, las propiedades de amortiguamiento y los comportamientos dependientes de la frecuencia del sistema. En este estudio, se utilizó la FRF para identificar las características dinámicas y extraer las frecuencias naturales de la estructura objetivo.
ACTUALIZACION DEL MODELO DE ELEMENTOS FINITOS (FE)
El modelo de elementos finitos es una representación numérica de una estructura física utilizada en análisis e simulaciones de ingeniería. Divide la estructura en elementos más pequeños, lo que permite analizar el comportamiento estructural complejo a través de elementos más pequeños y más fácilmente comprensibles. Sin embargo, el modelo de elementos finitos no puede reflejar las características de la estructura objetivo tal como es, ya que hay diferencias inevitables entre la estructura real y el modelo de elementos finitos teórico en términos de propiedades geométricas, propiedades del material y condiciones de contorno. En este sentido, se requiere una actualización del modelo de elementos finitos que minimice el error entre la estructura objetivo y el modelo de elementos finitos.
La actualización del modelo de elementos finitos (FE) es un proceso utilizado para mejorar la precisión de los modelos numéricos de FE ajustando sus parámetros basándose en datos experimentales, como se muestra en la Figura 3. En la actualización del modelo de FE, el modelo de FE inicial se compara con datos medidos obtenidos de sensores instalados en la estructura. Al ajustar iterativamente los parámetros del modelo, como las propiedades del material, las condiciones de contorno o las propiedades geométricas, el modelo de FE actualizado puede representar de manera más precisa el comportamiento dinámico de la estructura real. Las técnicas de actualización del modelo generalmente involucran algoritmos de optimización que minimizan la función objetivo, la cual cuantifica las diferencias entre el modelo de FE y las mediciones experimentales. La función objetivo se establece principalmente utilizando las características dinámicas de la estructura, como la frecuencia natural. Aunque el modelo de FE actualizado utilizando solo las frecuencias naturales no puede representar todos los comportamientos de la estructura objetivo tal como es, se puede utilizar para identificar los cambios en las características dinámicas debido a cambios en el sistema estructural. Una vez que se establece un modelo de FE actualizado que puede representar fielmente las características dinámicas de la estructura objetivo en su estado actual, también se pueden expresar las características dinámicas de defectos estructurales subsiguientes basándose en el modelo de FE de referencia. Este estudio adopta la técnica de actualización del modelo para entrenar una red de detección de daños mediante la generación de datos de simulación para varios defectos potenciales basados en el modelo de FE de referencia que replica las características dinámicas del sistema estructural objetivo.
RED NEURONAL PROFUNDA (DNN, por sus siglas en inglés)
El objetivo principal de este estudio es identificar daños en estructuras mediante cambios en las frecuencias naturales, las cuales son una de las características dinámicas de las estructuras. La frecuencia natural es un parámetro que está directamente relacionado con la rigidez y la masa de una estructura. Proporciona información significativa para identificar daños que pueden representarse como cambios en la rigidez. Sin embargo, la frecuencia natural representa las características globales de la estructura, las cuales dependen de interacciones complejas de varios factores dentro de la estructura y se determinan de manera diferente para cada sistema estructural. Especialmente para estructuras complejas, analizar la relación entre estos factores se vuelve más desafiante, lo que dificulta evaluar cambios en la rigidez a través de la frecuencia natural basándose en un enfoque analítico. Este estudio utilizó una red neuronal profunda (DNN), una red de inteligencia artificial capaz de proporcionar soluciones alternativas basadas en datos, para superar la limitación de dichos enfoques analíticos.
Como se muestra en la Figura 4, una red neuronal profunda (DNN) está compuesta por múltiples capas, que incluyen una capa de entrada, una o más capas ocultas y una capa de salida. La capa de entrada recibe los datos o características para el entrenamiento, los cuales luego se procesan a través de las capas ocultas. Las capas ocultas contienen nodos interconectados para extraer patrones complejos. Un nodo recibe entradas, realiza una operación de suma ponderada y luego obtiene un valor de característica en el nodo mediante una función de activación no lineal. Esto se puede representar matemáticamente como se indica en la ecuación (3).
En lo anterior, z representa la suma ponderada de las entradas (x) y sus pesos correspondientes (w), b es el término de sesgo (bias), σ denota la función de activación, y h representa la salida del nodo.Al apilar múltiples capas, las redes neuronales profundas (DNNs) pueden aprender representaciones jerárquicas de datos, lo que permite la extracción de características complejas. El flujo de información a través de la red se puede expresar como Ec. (4).
Aquí, hi representa la salida de la capa i, wi denota la matriz de pesos que conecta la capa i-1 con la capa i, y bi es el vector de sesgo de la capa i. Finalmente, la capa de salida produce la salida deseada según la Ec. (5) basándose en la información procesada de las capas anteriores.
Entrenar una DNN implica optimizar sus parámetros (pesos y sesgos) para minimizar la discrepancia entre las salidas predichas y las etiquetas de verdad. Esto se logra a través de un proceso llamado retropropagación, que calcula el gradiente de una función de pérdida definida con respecto a los parámetros de la red. Al aplicar un algoritmo de optimización, como el descenso de gradiente estocástico, la red actualiza iterativamente sus parámetros para mejorar su precisión de predicción.
Prueba de validación
La viabilidad del método propuesto se evaluó basándose en la prueba experimental. Se realizaron pruebas de vibración para extraer las características dinámicas de la estructura objetivo, las cuales luego se utilizaron para establecer un modelo FE de referencia que representara adecuadamente las características dinámicas de la estructura objetivo. Basándose en el modelo FE de referencia, se generaron varios modelos FE para condiciones de daño arbitrarias y se utilizaron para entrenar la red de aprendizaje profundo. El rendimiento de la red entrenada se evaluó aplicando las características dinámicas extraídas a través de la prueba en estructuras dañadas intencionalmente a la red.
Prueba experimental
Configuración experimental
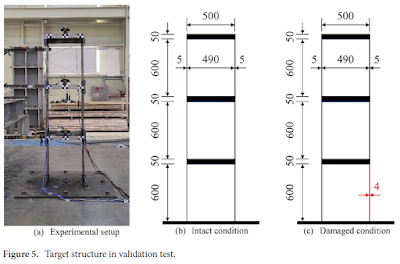
La prueba experimental se llevó a cabo en una estructura de marco de tres pisos como se muestra en la Fig. 5. El ancho y la profundidad de la estructura son ambos de 500 mm, y la altura total es de 1950 mm. Cada piso consta de una placa de acero con un grosor de 50 mm, que es sostenida por placas de pared con una altura de 600 mm y un grosor de 5 mm. Se consideró una condición de daño estructural al reducir el grosor en un lado de la placa de pared del primer piso en un 20%.
Resultados del experimento
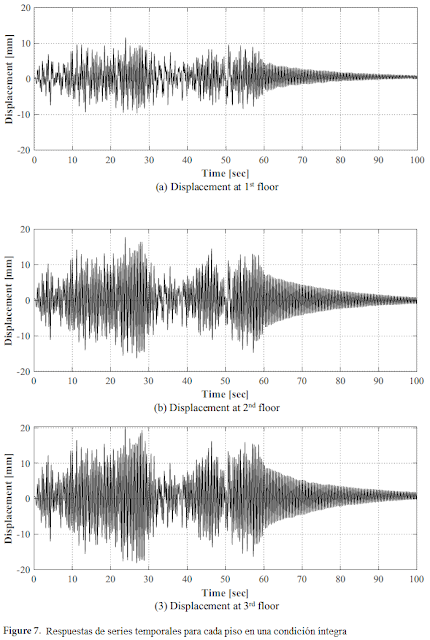
La Figura 7 muestra los desplazamientos de cada piso de la estructura en condición íntegra para el movimiento del suelo aplicado. La estructura fluctúa durante aproximadamente 60 s donde se aplica el movimiento del suelo, y posteriormente, muestra una disipación gradual de la excitación debido al amortiguamiento inherente de la estructura misma. Los desplazamientos máximos en cada piso fueron de 11.56 mm, 17.70 mm y 20.23 mm, respectivamente. Dado que la respuesta es causada por la entrada aplicada a la estructura y las características mecánicas de la misma, las propiedades estructurales pueden ser identificadas mediante el análisis de las respuestas de vibración ambiental.
Entre los diversos métodos para analizar datos de series temporales en el dominio de la frecuencia, este estudio utilizó la Función de Respuesta en Frecuencia (FRF por sus siglas en inglés) de las respuestas para identificar las características en el dominio de la frecuencia de la estructura. La Figura 8 muestra las FRFs para las respuestas de cada piso. Los puntos máximos en las FRFs pueden representar la frecuencia natural de la estructura, y se pueden identificar tres puntos en la figura. El primer punto máximo, que representa la primera frecuencia natural, apareció con mayor claridad. Aunque el segundo punto, que representa el segundo modo de vibración de la estructura, no fue bien reconocido en la FRF de la respuesta del segundo piso, pudo ser identificado a partir de las otras respuestas. Hay una cantidad relativamente grande de ruido incluido cerca de la tercera frecuencia natural, pero fue posible identificar los puntos máximos en todas las respuestas.
La Figura 9 muestra las respuestas de cada piso cuando se aplica movimiento del suelo a la estructura en la cual el daño está representado por la reducción del grosor de la pared de un lado del primer piso. Los desplazamientos máximos de cada piso fueron de 11.18 mm, 16.31 mm y 18.19 mm, respectivamente. En comparación con las respuestas de la estructura en condición íntegra como en la Figura 7, se considera que las características de la condición dañada son difíciles de identificar a través de las respuestas de la serie temporal. Más bien, la respuesta estructural en la condición íntegra exhibió una magnitud mayor en comparación con la condición dañada.
La Figura 10 muestra las Funciones de Respuesta en Frecuencia (FRFs) de las respuestas para analizar las características en el dominio de la frecuencia de las respuestas de la estructura en la condición dañada. Similar a los resultados de las FRFs para las respuestas de la estructura en la condición íntegra, se observó que a medida que aumentaba el rango de frecuencia, las FRFs contenían múltiples componentes de ruido. Sin embargo, parecía que se podía identificar cada punto máximo de todas las respuestas. Las frecuencias naturales de la estructura obtenidas a partir de las FRFs para las respuestas de la estructura en condiciones íntegras y dañadas se resumen en la Tabla 1. Las frecuencias naturales de la estructura en la condición dañada aparecieron con resultados reducidos del 7.89%, 5.29% y 1.75%, respectivamente, en comparación con las de la condición íntegra.
Análisis de elementos finitos
Descripción del modelo de elementos finitos (FE)
Se construyó un modelo de elementos finitos para la estructura probada con el fin de analizar las características de varias condiciones de daño para la estructura. El modelo de elementos finitos se modeló con elementos de viga 2D, ya que la estructura fue diseñada para resistir el movimiento lateral del suelo mediante el comportamiento de flexión de los miembros de pared. El análisis de elementos finitos se realizó utilizando ABAQUS, un programa de análisis estructural, y el modelo construido se muestra en la Figura 11. Las dimensiones geométricas del modelo son las mismas que las del modelo utilizado en la prueba experimental, y los valores mostrados en la Tabla 2 se aplicaron a las propiedades iniciales para el análisis estructural.
La Tabla 3 muestra los modos de forma y las frecuencias naturales del modelo de elementos finitos (FE). Los resultados mostraron que la masa efectiva acumulada hasta el tercer modo asciende aproximadamente al 98% para los modos laterales, lo que confirma su suficiencia para analizar las características dinámicas de la estructura. Sin embargo, el modelo de elementos finitos no puede replicar con precisión las características de la estructura real tal como está, ya que las propiedades estructurales aplicadas son diferentes de las de la estructura real. Debido a esta diferencia, el modelo de elementos finitos no es adecuado para analizar las características de las condiciones dañadas de la estructura objetivo, incluso si fue diseñado para la estructura como objetivo. El modelo de elementos finitos necesita ser aplicado con una actualización del modelo que lo optimice para que pueda representar las características de la estructura objetivo.
Modelo de elementos finitos de referencia
Para determinar el modelo de elementos finitos de referencia que sirve de base para analizar las características de las condiciones dañadas de la estructura objetivo, se aplicó un proceso de optimización básico al modelo de elementos finitos inicial. El modelo de referencia se determina como el modelo de elementos finitos que mejor representa las características dinámicas de la estructura objetivo a través de un proceso general de actualización del modelo. Tenga en cuenta que el modelo de referencia es una especie de modelo pseudo para estimar posibles daños a través de cambios en las características dinámicas de la estructura, y no representa el modelo objetivo en sí mismo que puede representar otros comportamientos como un comportamiento estático de la estructura objetivo. Las características dinámicas estructurales dependen de su rigidez y masa. Incluso para que el modelo represente una cierta característica dinámica, puede haber numerosos modelos posibles con diferentes combinaciones de rigidez y masa que la satisfagan. Con el fin de señalar que el modelo de referencia no está determinado de manera única y puede aplicarse como una variedad de modelos, este estudio utilizó varios modelos de referencia para evaluar la aplicabilidad del método propuesto.
En este estudio, los modelos de referencia se determinaron mediante dos procedimientos. En el primer paso, las propiedades aproximadas del modelo de referencia se determinan en función de la primera frecuencia natural al considerar el módulo de elasticidad y la masa de todo el modelo como valores únicos. En este paso se determinaron un total de tres modelos de referencia aproximados: dos modelos se determinaron considerando uno de los estimados iniciales del módulo de elasticidad y la masa como constantes y ajustando las otras variables, y el otro se determinó como un modelo que tiene una propiedad de compromiso entre los dos modelos. La Tabla 4 muestra las propiedades estructurales de los tres modelos de referencia determinados en el primer paso.
El segundo paso es el paso de ajuste fino para los modelos de referencia aproximadamente determinados. Las variables se expanden para cada piso, y se determinan para minimizar las diferencias en las 1.ª a 3.ª frecuencias naturales basadas en una serie de procesos de optimización. La función objetivo para la optimización se muestra en la Ec. (6).
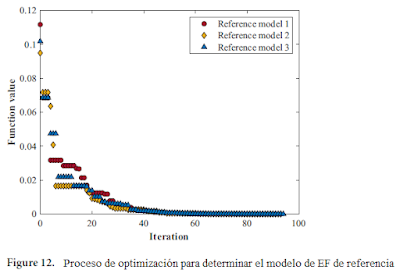
Aquí, [E] y [M] son el módulo de elasticidad y la densidad de masa de cada piso, y ωi y ω'i representan las frecuencias naturales extraídas a través del experimento de la estructura objetivo y basadas en el análisis de elementos finitos, respectivamente. m es el orden de las frecuencias naturales que se deben considerar, que se consideró hasta el 3er orden en este estudio. El problema de optimización en esta etapa para las propiedades estructurales con frecuencias naturales no es muy complicado, por lo que hay varios métodos que se pueden aplicar de manera relativamente simple. Para el ajuste fino del modelo de referencia, se aplicó el método Nelder-Mead en este estudio, y los resultados del proceso de optimización para cada modelo de referencia se muestran en la Figura 12.
Aunque la optimización comienza desde los valores iniciales que no son diferentes para cada piso derivados en el paso anterior, los valores finales obtenidos a través del proceso aparecen de manera diferente para los pisos. Las propiedades de los modelos de referencia derivados del proceso de ajuste fino se muestran en la Tabla 5. Mientras que los modelos tienen una distribución diferente de módulo de elasticidad y densidad de masa, todos representan características bastante idénticas en las frecuencias naturales. En adelante, el modelo de referencia determinado en esta etapa sería utilizado como una base que representa una condición íntegra para entrenar cambios en las características dinámicas causadas por los daños de la estructura objetivo.
Red de detección de daños
Este capítulo trata sobre el entrenamiento de redes de aprendizaje profundo para datos de análisis de elementos finitos dañados arbitrariamente generados en base a los modelos de elementos finitos de referencia determinados en el capítulo anterior. Suponiendo que no hay cambios en la masa dentro de la condición de daño estructural, las condiciones de entrenamiento se consideraron reduciendo arbitrariamente la rigidez de la placa de pared para cada piso del 100 al 50%. Los datos de entrenamiento para la red fueron generados a través del análisis de elementos finitos para modelos en condiciones dañadas arbitrariamente, en comparación con los modelos de referencia en una condición íntegra. El número de datos generados para la condición dañada es de 1000 para cada modelo de referencia. En el conjunto de datos total, se utilizó el 80% para el entrenamiento, el 10% para la validación del proceso de entrenamiento, y el 10% restante para las pruebas.
Configuración de la red
Estudio paramétrico
El rendimiento del entrenamiento de la red depende de varios factores. Para determinar la red óptima adecuada para el propósito del estudio, esta sección analiza los parámetros de la capa oculta, que son los parámetros significativos de la red utilizada en este estudio. Uno de ellos es el número de capas ocultas, que determina la profundidad y complejidad de la red. Aumentar el número de capas ocultas permite capturar relaciones más intrincadas en los datos, pero también aumenta el riesgo de sobreajuste. Otro es el número de nodos dentro de cada capa oculta. El número de nodos afecta la capacidad de la red para aprender y representar patrones en los datos. Más nodos pueden capturar características más matizadas, pero un número excesivo puede llevar al sobreajuste o aumentar la complejidad computacional. La Tabla 6 muestra los valores considerados en el estudio paramétrico. Los valores se determinaron como rangos en los que los parámetros representaban un rendimiento suficiente y sus efectos tendían a converger.
En el proceso de entrenamiento, una época representa una sola iteración en la que el modelo procesa todo el conjunto de datos una vez, y existe la necesidad de establecer una restricción en la época máxima para la terminación adecuada del entrenamiento. Una vez que se alcanza la época máxima, el proceso de entrenamiento generalmente se detiene, independientemente de si el modelo ha convergido completamente o no. La elección del valor de la época máxima depende de varios factores, como la complejidad del problema, el tamaño del conjunto de datos y los recursos computacionales disponibles. Establecerlo demasiado bajo puede resultar en un subajuste, donde el modelo no logra capturar los patrones subyacentes en los datos. Por otro lado, establecerlo demasiado alto puede provocar un sobreajuste, donde el modelo se vuelve demasiado específico para los datos de entrenamiento y tiene un rendimiento deficiente en nuevos datos. En este estudio, la época máxima se estableció en 10,000 por defecto, lo cual se encontró suficiente para que el rendimiento de entrenamiento de la red convergiera en el análisis preliminar. En su lugar, se aplicó la opción de paciencia para una detención temprana para evitar la repetición excesiva del proceso de entrenamiento. La opción hace referencia a esperar algunas épocas más antes de determinar que no hay más mejoras en el proceso de entrenamiento. Cuando la precisión de validación para los datos de validación aplicados en el proceso de entrenamiento no mejora durante varias épocas, el entrenamiento se detendría de forma temprana, y el valor se estableció en 200 en este estudio.
Un lote es el número de datos de entrenamiento que se procesan juntos en un único pase hacia adelante y hacia atrás durante cada iteración. La elección del tamaño del lote es un compromiso entre la eficiencia computacional y la convergencia del modelo. Un tamaño de lote más grande puede hacer un mejor uso de las capacidades de computación paralela y acelerar el entrenamiento, pero puede requerir más memoria. Por el contrario, un tamaño de lote más pequeño puede proporcionar una estimación más precisa del gradiente pero puede ser computacionalmente más lento. En este estudio, se aplicó un tamaño de lote de 32, que es un valor relativamente pequeño, porque el problema a resolver mediante el entrenamiento de la red no es tan complicado.
Durante el proceso de entrenamiento, los pesos del modelo se actualizan paso a paso según la tasa de aprendizaje, que controla el tamaño del ajuste de peso basado en el gradiente calculado. Si la tasa de aprendizaje es demasiado alta, es posible que el modelo sobrepase la solución óptima y no logre converger. Por otro lado, si la tasa de aprendizaje es demasiado baja, el proceso de entrenamiento puede ser lento o el modelo puede quedar atrapado en una solución subóptima. También se puede ajustar durante el progreso utilizando la opción de programación de la tasa de aprendizaje. Sin embargo, dado que el conjunto de datos y la complejidad del modelo no muestran variaciones significativas en este estudio, se adoptó una tasa de aprendizaje fija de 0.001 para mantener un esquema de actualización estable y consistente durante todo el procedimiento. Se ha utilizado ampliamente como un valor predeterminado en varias aplicaciones de aprendizaje profundo, lo que permite simplificar el proceso eliminando la necesidad de ajuste adicional de hiperparámetros y mecanismos de programación.
Cuando los datos disponibles son limitados, muestran desequilibrio o presentan variabilidad significativa que puede resultar en un entrenamiento sesgado, se puede considerar la validación cruzada para proporcionar una evaluación de rendimiento generalizada del modelo. Este estudio utilizó datos de simulación de análisis estructural para el entrenamiento, los cuales estaban distribuidos uniformemente en diversas condiciones. Además, el proceso de entrenamiento fue verificado aplicando un conjunto de datos de validación que era distinto de los datos de entrenamiento, y se confirmó que no ocurrió sobreajuste debido a sesgo entre los conjuntos de datos de entrenamiento y validación. Por lo tanto, considerando que los datos se aplicaron de manera relativamente clara para evitar un entrenamiento sesgado de la red, la validación cruzada no se consideró en este estudio.
Los modelos de referencia solo tienen diferencias en sus propiedades de material, y los cambios en sus características dinámicas debido a la disminución de la rigidez parecen similares. Por lo tanto, el estudio paramétrico se realizó basado únicamente en el modelo de referencia 1.
La Figura 14 muestra el rendimiento de la red para los parámetros considerados. Como se muestra en la Figura 14a, el rendimiento de la red tiende a converger cuando el número de capas ocultas es aproximadamente 5, aunque varía en cierta medida según el número de nodos en la capa oculta. La Figura 14b muestra que, si bien existe una tendencia a mejorar el rendimiento de la red en cierta medida con un aumento en el número de nodos, la mayoría de las redes representan un rendimiento satisfactorio, excepto en los casos donde el número de nodos es demasiado pequeño, como 10. Según los resultados de la Figura 14c, este estudio determinó que el número de capas ocultas y nodos sería de 5 y 2000, respectivamente, para la detección de daños estructurales mediante el entrenamiento de la red con datos de elementos finitos dañados arbitrariamente.
Resultados del entrenamiento
La red determinada en la sección anterior se aplicó a cada modelo de referencia y se entrenó para las frecuencias naturales de los modelos de elementos finitos con la rigidez de cada piso reducida arbitrariamente del 50 al 100%. El rango de reducción de rigidez se puede ajustar para una evaluación integral de varios escenarios de daño según el propósito. Se generaron un total de 1000 modelos dañados para cada modelo de referencia, proporcionando un conjunto diverso de datos de entrenamiento y prueba. Para evaluar el entrenamiento de la red, el 80% de los modelos generados se utilizaron para entrenar la red, mientras que el 20% restante se reservó para probar sus capacidades.
La Figura 15 muestra los resultados para los datos evaluados. Los resultados demuestran que la red ha sido entrenada adecuadamente, como lo indican los valores de RMSE logrados de menos del 0.85% para todos los modelos de referencia. Los bajos valores de RMSE indican una fuerte correlación entre las rigideces predichas y reales, lo que valida aún más que la red puede representar un rendimiento generalizado sobre una variedad de degradaciones de rigidez.
Este estudio adopta los modelos de elementos finitos de referencia para simular las características dinámicas de la estructura sometida a daños, como se observa en la prueba experimental. Las frecuencias naturales obtenidas de la prueba experimental se aplican como entradas para las redes neuronales entrenadas correspondientes a cada modelo de referencia, y los resultados se muestran en la Figura 16.
Los resultados indican que todas las redes proporcionan estimaciones razonablemente precisas de la rigidez cuando se aplican las frecuencias naturales de la estructura en una condición íntegra. Aunque la red para el modelo de referencia 2 muestra el mayor error, estimando la rigidez de la placa de pared del segundo piso como 99.27%, se puede considerar un error aceptable para el propósito del estudio.
Durante la prueba experimental, la condición dañada de la estructura se representó reduciendo el grosor de una de las placas de pared del primer piso en un 20%. Al no tener en cuenta la disminución de la masa resultante del grosor reducido de la placa de pared, se puede evaluar como equivalente al 75.6% de la rigidez del primer piso en comparación con la condición íntegra. Los resultados para la estructura en condición dañada demuestran que también puede exhibir un rendimiento adecuado en la estimación de la distribución de rigidez de la estructura bajo tales condiciones dañadas. Aunque la rigidez de la placa de pared del tercer piso se estimó relativamente más baja que la de la condición íntegra, aún indica que la rigidez está suficientemente asegurada en comparación con el primer piso, en el cual se aplicó la condición de daño real. Además, los valores estimados para la rigidez del primer piso muestran resultados relativamente precisos en comparación con sus valores ideales, lo que indica un potencial prometedor para la aplicación práctica en la detección de daños estructurales.
Los resultados también confirmaron que los modelos de referencia con diferentes propiedades de material pueden usarse de manera equivalente para estimar el daño estructural basado en las características dinámicas de una única estructura objetivo. Aunque no pueden reflejar completamente el comportamiento de la estructura, pueden utilizarse para el análisis de características dinámicas dominadas por la rigidez y la masa de la estructura. Esto indica que existen diversos modelos de elementos finitos que pueden representar las características dinámicas de una sola estructura, a menos que se trate de analizar el comportamiento completo de la estructura.
Conclusión
Este estudio propuso nuevos métodos de detección de daños utilizando actualización de modelos, simulación de análisis estructural y aprendizaje profundo. La red de aprendizaje profundo se utilizó para la estimación confiable de diversas condiciones de daño, y la actualización del modelo de elementos finitos se utilizó para mejorar la aplicabilidad de los datos de entrenamiento basados en simulación a la estructura objetivo real. El método propuesto se validó mediante pruebas experimentales en una estructura de tres pisos, y se llegaron a las siguientes conclusiones.
I. El modelo de elementos finitos de referencia para la detección de daños estructurales derivado de la actualización del modelo de elementos finitos puede tener varias propiedades estructurales como valores iniciales. Esto implica la presencia de múltiples modelos de elementos finitos que pueden representar eficazmente las características dinámicas de la estructura objetivo, en lugar de indicar un fallo del proceso de actualización del modelo para converger a un solo modelo.
II. El modelo de elementos finitos de referencia tiene la intención de representar los cambios en las características dinámicas resultantes de cambios en el sistema estructural, en lugar de replicar todos los comportamientos de la estructura objetivo. Se ha confirmado que los datos de entrenamiento generados en base a dicho modelo de referencia pueden representar suficientemente los cambios en las características dinámicas causados por daños estructurales en la estructura objetivo.
III. El método propuesto mostró un error promedio de aproximadamente 0.29% y 1.58% para la distribución de rigidez de las condiciones íntegras y dañadas de la estructura objetivo, respectivamente, lo que proporciona evidencia de la efectividad del método propuesto.
Dado que este estudio se realizó para una estructura de tres pisos relativamente simple y se aplicó un nivel extenso de daño, fue posible identificar suficientemente el daño utilizando solo algunas frecuencias naturales como características de entrada. Además de la frecuencia natural, existen diversas características de comportamiento como la forma del modo y la energía modal que se pueden usar como características de entrada. Además, más allá de los métodos en el dominio de la frecuencia aplicados en este estudio, se pueden utilizar otras técnicas avanzadas como los métodos en el dominio del tiempo para características de entrada adicionales. Para abordar estructuras objetivo más complejas o lograr un mayor nivel de precisión en la detección de daños, puede ser necesario considerar el empleo de tales características de entrada adicionales o métodos avanzados.
Disponibilidad de datos
Los conjuntos de datos utilizados y/o analizados durante el estudio actual están disponibles del autor correspondiente bajo solicitud razonable.