CAP. 5
ESPECTROS DE RESPUESTA
5.1 INTRODUCCION
- En los Capítulos 2 y 3 se discutieron los diferentes sistemas dinámicos de 1GDL y la manera de obtener la respuesta a una excitación dinámica, ya sea por medio de la solución trascendental de la integral de convolución, o por medio de técnicas numéricas.
- En el Capítulo 4 se vió la forma que tienen los registros acelerográficos obtenidos de los movimientos del terreno inducidos por un sismo. En general, estos son movimientos que varian aleatoriamente en el tiempo.
- El siguiente paso es obtener la respuesta de un sistema dinámico de 1GDL a uno de estos registros acelerográficos.
5.2 OBTENCION DEL ESPECTRO DE RESPUESTA
5.3 RELACION ENTRE Sa, Sv y Sd
Dado que hay una aproximación en la ecuación anterior, el espectro de velocidades obtenido de multiplicar cada ordenada del espectro de desplazamientos por el valor ω se conoce con el nombre de espectro de pseudo-velocidades, y de igual manera el espectro de aceleraciones que se obtiene al multiplicar el espectro de desplazamientos por el valor de ω² se conoce con el nombre de espectro de pseudo-aceleraciones.
- Espectro de pseudo-velocidades
- Espectro de pseudo-aceleraciones
5.6 RELACION ENTRE LAS DIFERENTES COMPONENTES
Los movimientos sísmicos son tridimensionales y extremadamente aleatorios.
El acelerógrafo solo registra los movimientos traslacionales en tres direcciones, dos horizontales y una vertical, como muestra la figura 5-11. No necesariamente el movimiento se limita a efectos traslacionales.
Los acelerógrafos no registran los parámetros rotacionales del movimiento. Estos se pueden determinar utilizando grupos de acelerógrafos localizados cerca y con un registro de tiempo unificado, lo cual permite calcular las velocidades angulares de los efectos rotaciones del movimiento, lo cual, desafortunadamente, solo se logras en muy contadas ocasiones.
La localización del instrumento es totalmente arbitraria y no siempte se hace con uno de sus ees coincidiendo con el norte.
En general las componentes horizontales tienen valores de aceleración mayores que la componente vertical. La figura 5-12 muestra el espectro para la componente vertical del temblor de El Centro de 1940, comparando con una de las componentes horizontales.
Si para cada instante de los acelerogramas de la figura 5-13, se dibuja el vector de aceleraciones en un plano, se obtiene el gráfico presentado en la figura 5-14.
El movimiento, es extremadamente aleatorio en sus aspectos direccionales, aunque hay ciertas preferencias, como en este caso hacia la dirección N15W; los cuales tienen que ver con:
- la localización del instrumento con respecto a la falla que causó los movimientos,
- aspectos de la geología local,
- el tipo de mecanismo focal,
- y otros, sobre los cuales se conoce muy poco en la actualidad.
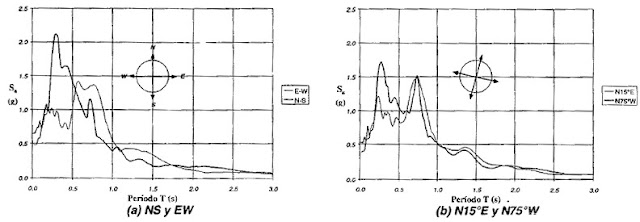
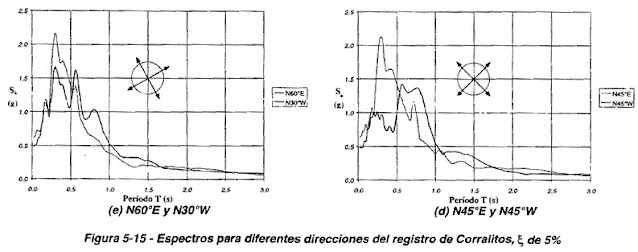
Esta variabilidad direccional conduce a que los espectros que se calculan para cada una de las direcciones principales, y para cualquier dirección que se recomponga de las dos direcciones principales, sean diferentes.
En la figura 5-15 se muestran los espectros calculados para el mismo registro de Corralitos, para componentes en direcciones que van variando desde EW hasta WE de 15° en 15°. Allí puede verse que los espectros varian apreciablemente.
5.7 ESPECTROS DE ALGUNOS SISMOS
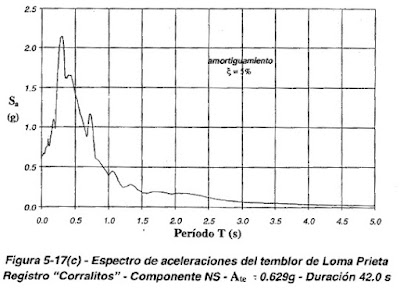
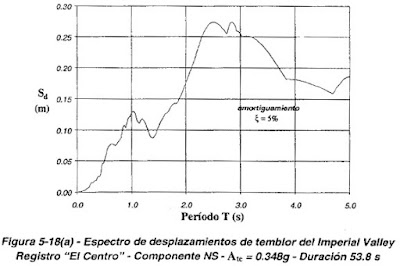
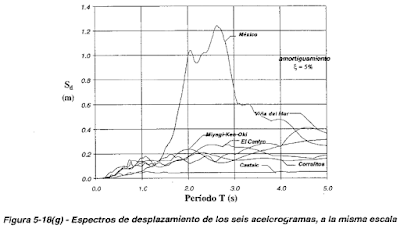
En la figura 5-17 se presentan los espectros de aceleraciones y en la figura 5-18 los espectros de desplazamientos de los seis acelerogramas de la figura 4-10, calculados para un amortiguamiento del 5% del crítico.
Con los registros presentados se cubre una gama amplia de movimientos sísmicos, con situaciones de
- suelo blando, con periodos preponderantemente largos, como es el caso de los registros de México y Miyagi,
- con alto contenido de periodos cortos, como son El Centro, Castaic y Corralitos,
- y con preponderancia a los periodos intermedios como es el caso de Viña del Mar.
5.8 ESPECTROS DE FOURIER
El contenido frecuencial de los movimientos sísmicos se puede identificar convirtiendolo del dominio del tiempo al dominio de la frecuencia, por medio de un procedimiento que consiste en representarlo por medio de series de Fourier.
A modo de ejemplo del uso del espectro de Fourier, se genera una onda que es la superposición de dos ondas sinusoidales, una con periodo de 2 s y otra que cabalga sobre ella con un periodo de 0.25 s. En la figura 5-19 se muestran tanto el acelerograma como su espectro de Fourier que se obtiene.
El espectro de Fourier asocia la energia que lleva la onda en cada uno de los periodos, con el máximo para un periodo de 2 s, el segundo pico para un periodo de 0.25 s.
En la figura 5-20 se presenta el espectro de Fourier del sismo de El Centro de 1940, y en la figura 5-21 el del sismo de México de 1985.
La amplitud del espectro de Fourier tiene unidades de longitud sobre tiempo. En este caso las amplitudes se obtuvieron utilizando el acelerograma como fracción de g, por lo tanto las unidades de la amplitud son segundo sobre g; y al multiplicar la amplitud por la aceleración de la gravedad se obtienen unidades m/s.
Puede verse que las mayores amplitudes se presentan para periodos menores de 1 s en el caso de El Centro (periodos cortos), como muestra la figura 5-20.
En el caso de México (suelo blando, periodos largos), se observa que la máxima amplitud se presenta para un periodo cercano de 2 s y que las amplitudes para periodos cortos son muy pequeñas. Esto se debe a que el registro de México es un registro que fue amplificado por el suelo en el lugar del registro, variando las amplitudes con respecto al registro en roca.
En la sección 2.6 se indicó que la energía que impone una aceleración en su base a una estructura tienen una relación con el espectro de Fourier. Aunque tiene gran importancia la definición de la energía que disipa el amortiguamiento dentro de un sistema, este aspecto adquiere caracteristicas totalmente diferentes, en su orden de magnitud, cuando entra en juego la respuesta inelástica del sistema.
La interpretación de los valores de la amplitud de los espectros de Fourier no tiene gran valor desde el punto de vista práctico de ingenieria de diseño, no obstante, es una gran herramienta para la definición de los periodos de vibración dominantes en un acelerograma, especiualmente en el estudio de los efectos de las ondas sísmicas debida a la estratificación del suelo en el lugar de interes.