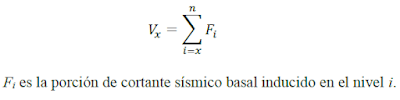CAPÍTULO 7
METODOS DE ANALISIS SISMICO
Artículo 21. ANALISIS ESTATICO
El método de análisis estático solo puede usarse en los siguientes casos:
1. En zonas sísmicas con S0 ≤ 0.10
2. Estructuras sin irregularidades y que no excedan los 30 m de altura.
En el método de análisis, la acción sísmica se asimila a un sistema de fuerzas cuyos efectos se calculan siguiendo los procedimientos de la estática.
P I - Fuerza de corte basal
La fuerza de corte basal V está dada por:
donde Cs es el coeficiente de respuesta sísmica igual a:
W = Peso sísmico efectivo.
El valor calculado del coeficiente de respuesta sísmica no debe exceder:
y tampoco debe ser menor a:
adicionalmente, para estructuras localizadas donde S0 es mayor a 0.32, Cs no debe ser menor que:
P II - Periodo fundamental de la estructura
El periodo fundamental de la estructura T en la dirección bajo consideración será establecido usando un análisis debidamente justificado que tome en cuenta las propiedades estructurales y características de deformación de los elementos resistentes. El periodo fundamental T no debe ser mayor al producto del coeficiente Cu y el periodo fundamental aproximado Ta. Como una alternativa al análisis para la determinación del periodo fundamental, se permitirá usar directamente el periodo fundamental aproximado Ta.
P III - Periodo fundamental aproximado
El periodo fundamental aproximado Ta puede ser calculado con la siguiente ecuación:
donde hn es la altura de la estructura y los coeficientes Ct y x se encuentran en la Tabla 7-2.
Alternativamente,
- Para estructuras de hasta 12 pisos, en que cada piso tiene una altura de por lo menos 3 metros y cuando el sistema resistente de las fuerzas sísmicas consiste solamente en pórticos resistentes a momentos de hormigón o acero, se puede calcular el periodo fundamental aproximado Ta, en segundos, con la siguiente ecuación:
siendo N es el número de pisos.
- El periodo fundamental aproximado Ta para mampostería o para muros de cortante de hormigón en estructuras de hasta 36 metros de altura, puede ser calculado con la siguiente expresión:
P IV - Distribución vertical de fuerzas sísmicas
La fuerza sísmica lateral Fx, inducida en cualquier nivel será determinada con la siguiente ecuación:
P V - Distribución de fuerzas horizontales
El cortante de diseño sísmico en cualquier piso Vx será determinado según la siguiente ecuación:
El cortante de diseño sísmico en cada piso Vx será distribuido a los elementos verticales del sistema resistente a fuerzas sísmicas del piso en consideración, basándose en la rigidez lateral relativa de los elementos verticales resistentes y del diafragma.
P VI - Torsión inherente
Para diafragmas rígidos la distribución de fuerzas laterales debe considerar el efecto del momento torsional inherente Mt que resulta de la excentricidad entre el centro de masa y el centro de rigidez.
Para diafragmas flexibles, la distribución de fuerzas a los elementos verticales debe tomar en cuenta la posición y distribución de las masas soportadas.
P VII - Torsión accidental
Cuando los diafragmas son rígidos el diseño debe incluir el momento torsional inherente Mt resultante de la distribución de las masas de la estructura más el momento torsional accidental Mta causado por un desplazamiento asumido del centro de masa a cada lado de su ubicación, se asume que este desplazamiento es igual al 5% de la dimensión de la estructura perpendicular a la dirección de las fuerzas aplicadas.
Cuando las fuerzas producidas por el sismo son aplicadas de forma concurrente en las dos direcciones ortogonales, el desplazamiento del centro de masa no necesita ser aplicado en ambas direcciones ortogonales al mismo tiempo, pero será aplicado en la dirección que produce el efecto más desfavorable.
P VIII - Resistencia al vuelco
La estructura será diseñada para resistir los efectos de vuelco causados por las fuerzas sísmicas determinadas en el Capítulo 5.
P IX - Determinación de la deriva de piso
La deriva de piso Δi, será calculada como la diferencia de los desplazamientos en los centros de masa superior e inferior del piso en consideración dividida entre la altura del piso.
Cuando los centros de masa no están alineados verticalmente, se permite calcular el desplazamiento inferior del piso basado en la proyección vertical del centro de masa superior.
Para estructuras que tienen irregularidad torsional, la deriva de piso será calculada como la mayor diferencia en desplazamientos de puntos alineados verticalmente en la parte superior e inferior del piso bajo consideración, a lo largo de cualquier borde de la estructura.
El desplazamiento δx en el nivel x, usado para el cálculo de la deriva de piso Δi, será determinado según la siguiente ecuación:
P X - Cortante basal mínimo para el cálculo de derivas de piso
El análisis elástico del sistema resistente a fuerzas sísmicas para el cálculo de las derivas deberá realizarse usando las fuerzas sísmicas de diseño prescritas en el Capítulo 5.La ecuación:
no necesita ser considerada para el cálculo de las derivas.
P XI - Periodo para el cálculo de las derivas de piso
P XII - Efectos P-Delta
Los efectos P-Delta en cortantes y momentos de piso, así como las derivas de piso inducidas por estos efectos, NO necesitan ser considerados cuando el coeficiente de estabilidad (θ), determinado por la siguiente ecuación, es igual o menor que 0.10.
El coeficiente de estabilidad no debe ser mayor que:
Siendo β la relación entre la demanda y la capacidad a cortante para el piso entre los niveles x y x-1. Conservadoramente, esta relación puede tomarse igual a 1.
Cuando el coeficiente de estabilidad es mayor a 0.10 pero menor o igual a θmáx, el incremento relacionado a los efectos P-Delta sobre los desplazamientos y fuerzas será determinado por un análisis racional. Alternativamente, se permite multiplicar los desplazamientos y fuerzas por 1/(1–θ).Cuando θ es mayor que θmáx, la estructura es potencialmente inestable y debe ser rediseñada.
Cuando los efectos P-Delta son incluidos en un análisis automático, la ecuación:
debe ser satisfecha, sin embargo, cuando se usan los resultados del análisis P-Delta, el valor de θ calculado según:
Puede dividirse por (1–θ) antes de ser comparada con θmáx.
Artículo 22. ANALISIS MODAL ESPECTRAL
P I - Número de modos
Se realizará un análisis dinámico para determinar los modos y periodos naturales de vibración de la estructura.
El análisis incluirá el número suficiente de modos de vibración de manera que se alcance por lo menos la participación modal del 90 % de la masa sísmica en cada dirección horizontal ortogonal.
P II - Parámetros de respuesta modal
El valor de cada parámetro de diseño de interés, incluyendo derivas de piso, reacciones en apoyos y fuerzas en elementos individuales para cada modo de respuesta, serán calculados usando las propiedades de cada modo y el espectro de respuesta definido en el Capítulo 6 dividido por la cantidad R/Ie.
El valor de los desplazamientos y de las derivas deberá ser multiplicado por Cd/Ie.
P III - Parámetros de respuesta combinada
El valor de cada parámetro de interés calculado para los distintos modos deberá ser combinado utilizando el método de la Raíz Cuadrada de la Suma de Cuadrados (SRSS), el método de Combinación Cuadrática Completa (CQC), el método de Combinación Cuadrática Completa modificado por el (ASCE 4, 1998) (CQC-4), o cualquier procedimiento equivalente justificado. Para aquellos casos, en los que modos próximos tengan correlación cruzada significativa en la respuesta traslacional o torsional, se deberá utilizar el método CQC o el CQC-4.
P IV - Valores del cortante basal modal y cortante estático
Deberá calcularse un cortante basal modal Vt mediante las combinaciones modales en cada una de las direcciones horizontales ortogonales. También deberá calcularse un cortante basal estático V en cada una de las direcciones horizontales ortogonales usando el periodo fundamental T y los procedimientos descritos en el Método Estático de la sección Artículo 21.
P V - Escalado de fuerzas
Cuando la respuesta combinada para el cortante basal modal Vt, resulte menor que el 65 % del cortante basal V calculado según lo indicado en la sección P I1, debe realizarse una corrección modificando el valor de R, de la siguiente manera:
P VI - Escalado de derivas
Solo se considerará el escalado de derivas para estructuras localizadas donde S0 > 0.32, en este caso el coeficiente basal del método estático debe ser
Y cuando el cortante basal combinado del método modal Vt es menor a Cs∙W, las derivas deben ser amplificadas adicionalmente por:
P VII - Amplificación por torsión accidental
La distribución del cortante horizontal deberá estar en concordancia con el procedimiento de distribución del método de fuerza lateral equivalente (sección P V), excepto que la amplificación por torsión no sea requerida donde los efectos de torsión accidental son incluidos en el modelo de análisis dinámico.
Los efectos P-Delta deberán ser determinados en concordancia con la sección P XII del método estático. El cortante basal utilizado para determinar los cortantes por piso y las derivas de piso deberá ser determinado en concordancia con la sección Artículo 21.
P IX - Interacción suelo-estructura
Las solicitaciones transferidas al suelo por las fundaciones pueden suponer que la estructura esta empotrada en la base o alternativamente considerar la flexibilidad del sistema de fundación acorde al Capítulo 8.
P X - Modelado de la estructura
La estructura debe ser modelada en tres dimensiones (3D). El modelo debe incluir la rigidez y resistencia de todos los elementos significativos para la distribución de fuerzas y deformaciones en la estructura, representando la distribución espacial de masa y rigidez a través de la estructura. En el caso de entrepisos que se consideren como diafragma rígido, por lo menos tres grados de libertad deben ser usados en cada piso, dos grados de libertad horizontales ortogonales y un grado de libertad rotacional con eje vertical.
Cuando el diafragma de piso no es rígido, el modelo debe representar la rigidez del diafragma en la respuesta dinámica de la estructura.Artículo 23. ANALISIS LINEAL TIEMPO-HISTORIA
P I - Requerimientos generales
El análisis lineal tiempo-historia consiste en el análisis de un modelo matemático lineal de la estructura, que determina su respuesta ante varios registros de aceleración, a través de métodos de integración numérica. Los registros de aceleración deben ser compatibles con el espectro de respuesta de diseño del lugar de emplazamiento de la obra.
P II - Requerimientos generales para el modelado
El modelo matemático de la estructura debe cumplir con lo especificado en la sección P VIII.